Double error!
What every engineer needs to know about floating-point errors in every computer
Disclaimer
This post is about to get way too technical. I could opt to spit out “do this, not that” or to explain how it works. However, I won’t make the choice for you. I’ll give you the TL;DR option at the end of the page. Feel free to skip to the last section if you don’t have enough time to read this, but this content shouldn’t intimidate an engineer. It’s just a bit lengthy.
If you choose to read everything, there will be NOTHING new in the TL;DR section.
If you are looking for how to represent and store decimal numbers accurately, see [https://blog.pplupo.com/2021-12-07-Implementation-of-Decimal-Numbers/).
SEM Blog | Implementation of Decimal Numbers
What is a floating-point number?
According to the IEEE 754:2019, a floating-point number is a finite or infinite number that is represented in a floating-point format.
The floating-point format is a standard approximation to represent numbers in a finite number of bits. As with any approximation, it is not without loss of precision.
The standard is based on a triple, one bit for the sign, a certain number of bits for the exponent, and the remainder for the mantissa (a.k.a. significant or fraction).
As an example, here is a 32-bit floating-point number (float):

A 64-bit floating-point number (double) would have a different allocation of bits for the triple:
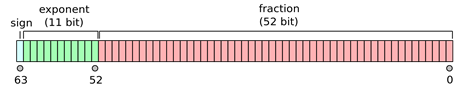
The name “floating-point” comes from the fact that the difference in representation between binary numbers such as 1.1101011101 and 111.01011101 would only depend on where the point is, defined by the exponent. Therefore we have a point that can float around to different positions in the mantissa, defining different numbers and changing how precise the number can be.
Note
This defines how decimal numbers are represented in binary computers, not in Java or C++ or any specific language. This is how it works in memory, therefore any binary computational system is impacted by this, may it be a programming language or a database.
Precision Loss
The precision loss comes from the fact that we cannot represent all decimal numbers in binary form.
If you remember that in decimal 0.4 is the same as 4 x 10⁻¹, you will understand that in base 2, the number 0.1 translates to 1 x 2⁻¹, which in decimal is equivalent to 0.5. This means that, because we only have digits 0 and 1, we can only express in binary, decimals that can be represented as sums of powers of -2.
While these numbers work just fine:
Decimal 2.0 2.5
Binary 10.0 10.1
If you try to store the decimal 2.6 you will see the problem because 0.6 cannot be represented as a power of 2:
10.1100 = 2.75, which is greater than 2.6.
10.1010 = 2.625, which is still greater than 2.6.
10.1001 = 2.5625, which is smaller than 2.6.
There is no combination of any finite number of binary digits that will correctly represent X.6 (where X is an integer part).
If you want to see what decimal and binary values are actually stored in the memory when you try to store one of these “unsupported” decimals, have fun here: Base Convert: IEEE 754 Floating Point.
Coding around the precision loss
So, knowing that there is a loss in precision, we have to account for that when developing code that uses floating-point representations.
Comparison
Note
If I could choose ONE thing for you to remember out of all this document, this would be it. How to compare floating-point numbers.
Knowing that 3.003 x 2.002 = 6.012006, one would expect that the following comparison would return true:
System.out.println(6.012006 == 3.003 \* 2.002); //prints falseBut knowing the limitation of the floating-point representation, we know that some of these numbers may not (or will not) be accurately represented. As a matter of fact, the multiplication of 3.003 x 2.002 only yields 6.012006 in decimal. In binary, the result will be 6.0120059999999995. Therefore, the comparison will return false.
The correct way to compare floating-point representations of decimal numbers is by defining an error threshold. For instance, given that both 3.003 and 2.002 have only 3 decimal places, it should be ok to dismiss anything smaller than 10⁻⁷, so the threshold is defined as 10⁻⁶:
System.out.println(6.012006 - 3.003 \* 2.002 < 0.000001); //prints trueSimple examples with sums and subtractions like
System.out.printf("%.16f\\r\\n",0.7+0.1); // DOESN'T print 0.8. It prints 0.7999999999999999.
System.out.printf("%.16f\\r\\n",0.8-0.09); // DOESN'T print 0.71. It prints 0.7100000000000001.Because they are sums and subtractions, the result of the operations should keep the precision the same as the original values, therefore you shouldn’t have to sum the number of decimal places of each. Just take the highest number of decimal places, as a general rule.
System.out.println(0.8 - (0.7+0.1) < 0.1); // prints true
System.out.println(0.71 - (0.8-0.09) < 0.01); // prints trueThis would be the correct way to compare these numbers. So never compare floating-point numbers directly when they do not represent binary numbers. Always define a threshold.
Also, be aware of >= and <=, since these operations also involve equality. You may expect that the comparisons might return true when the numbers are equal but they might not be equal (even when they should).
Note
Rule of thumb to define the threshold:
First method: Mathematically, if you are multiplying or dividing numbers, multiply the number of decimal digits of each operand. If you are summing or subtracting, take the highest number of digital places of each operand.
Second method: If your application doesn’t care for such precisions and there is a standard number of digits because of business rules or constraints, use that.
Which method you should apply will depend on the context. If you are displaying money figures and your application is determining a value to be displayed, apply the second method. If you are in the very same application but defining the size of images, the second method would not be relevant. Be aware of what the numbers mean in your code.
Summation
Summing floating-point numbers is usually straightforward, but it can easily become nightmarish. The problem starts with the concept of adding numbers that have a very large difference in the exponent.
When exponents are different, the mantissa positions represent different powers of 2. For instance:
100 (exp) x 001 (mantissa) = 00.1 (binary) (which is 0.5 in decimal)
10 (exp) x 001 (mantissa) = 0.01 (binary) (which is 0.25 in decimal)
Therefore, the exponents need to match before the sum can be performed. When one of the exponents is too high and the other is too low, the matching will cause a shift in the bits of the lower one and significant bits can be lost. Actually, all of them can be lost. Just imagine if the small number has just a few bits set to 1 at the end of the mantissa and now you need to increase the exponent. As you increase the exponent, you will have to introduce zeros at the left, pushing the 1’s at the right out.
While in some circumstances like when you simply need to sum 2 very different values have no workaround, accumulators may require special treatment.
An accumulator is when you accumulate the values in a variable inside a loop, such as:
while (condition) {
accumulator = accumulator + value;
}The problem with this approach is that the accumulator will grow continuously, and the last values may be lost if they are too small. For this purpose there are specific methods that calculate the loss at each sum, accumulate them separately and add them back at the end or adopt other strategies to minimize the error.
If you find yourself in need of such a solution, look for libraries that provide this implementation out-of-the-box. You will have to look for things like Shewchuk’s “Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates”, Kahan summation algorithm, and Pairwise summation.
A very interesting Summarizer was posted here: https://github.com/martinus/java-playground/blob/master/src/java/com/ankerl/math/Summarizer.java
It’s a port from this Python implementation: Binary Floating-Point Summation Accurate To Full Precision (Python Recipe). It’s not perfect in some edge cases, though.
Rounding
Operations with floating-point represented numbers are subject to rounding (when needed). The rounding strategy is to round to the nearest even number (or “Round to Even”) as it is the method that statistically avoids the accumulation of rounding errors. This is also defined as part of the IEEE 754:2019 specification.
Percentages (Largest Remainder Method)
It is common to see percentages with partials that sum up to 99.99% or, more rarely, to 100.01%. These are often errors caused by improper rounding of partials or floating-point representation errors. If you have such errors in screens, reports, etc, please look for an implementation of the “Largest Remainder Method” as it is intended to correct the distribution by changing the partials the least possible and keeping their proportion as close as they can be so that the sum can get to exactly 100%.
Implementation in different programming languages and databases are posted here: Implementation of Decimal Numbers
SEM Blog | Implementation of Decimal Numbers
TL;DR
Note
If you read everything so far, you can skip this. There will be nothing new. If you skipped to this section, please know that not only you are missing the reasons why you should do these things this way but also some other directions on how to perform less common operations.
Never compare double or float numbers directly.
You would expect this to be true, but 3.003 * 2.002 will not result in 6.012006 (even if your calculator says so).
System.out.println(6.012006 <= 3.003 \* 2.002); //prints falseAlways use a threshold:
System.out.println(6.012006 - 3.003 \* 2.002 < 0.000001); //prints trueRule of thumb to define the threshold:
First method: When doing math, when you sum 2 numbers, the number of decimal digits in the result is the higher between the 2 parcels:
4 digits (1.0001) + 2 digits (1.01) = 4 digits(2.0101).
When you multiply, you sum the number of digits from the parcels:
3 digits (3.003) x 3 digits (2.002) = 6 digits ( 6.012006).
So, mathematically, if you are multiplying or dividing numbers, sum the number of decimal digits of each operand. If you are summing or subtracting, take the highest number of digital places of each operand.
Second method: If your application doesn’t care for such precisions and there is a standard number of digits because of business rules or constraints, use that.
Which method you should apply will depend on the context. If you are displaying money figures and your application is determining a value to be displayed, apply the second method. If you are in the very same application but defining the size of images, the second method would not be relevant. Be aware of what the numbers mean in your code.
Accumulations
while (condition) {
accumulator = accumulator + value;
}When you are accumulating values (summing values in a loop) and either the accumulator variable, the accumulated values (or both) are declared as double or float, it might result in loss of values (values not being added).
There are proper ways to do this without loss, like Shewchuk’s “Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates”, Kahan summation algorithm, and Pairwise summation.
Implementation in different programming languages and databases are posted here: Implementation of Decimal Numbers
SEM Blog | Implementation of Decimal Numbers
If you like this post, please share it (you can use the buttons in the end of this post). It will help me a lot and keep me motivated to write more. Also, subscribe to get notified of new posts when they come out.
